빅데이터 특강의 수료증을 받기 위해서는 과제를 제출해야 했다.
그래서 이번 시간에 과제를 했다. 밑에 나온 코드들은 다 R로 작성을 했다.
문제는 총 네개였다.
문제 풀이 전에 잠시 강조할 것이 있다.
강사 선생님께서 코드를 작성할 때 꼭 주의해야한다고 말씀해주신 게 있다. setwd()와 getwd()를 늘 먼저 해야한다고 하셨다.
또 강사 선생님께서 R은 멍청한 프로그램이라고 했다. 그러나 library를 어떻게 쓰느냐에 따라 똑똑해질 수 있다고 했다.
아래 두 개를 늘 새기고 코드를 작성했다.
1. getwd()를 해서 자신의 주소를 알아야 한다.
2. Hmisc, prettyR를 설치하고 library로 깔자.
문제1. 비율 분석을 이용하기

‘신공정은 기존 공정에 비해서 불량률이 변화하였을 것이다.’라는 가설을 세운다.
변주 이름이 불량률이어서 문제 해석이(불량률이 변화하였는지) 어려웠다. 처음에 나는 두 개 다 범주형 변수라서 카이제곱 테스트를 했다. 후에 정답을 보니 비율 분석으로 푼 것을 확인했다.
두 집단 비율 차이 분석을 하기 위해서는 이표본 비율 검정을 사용한다.
factory = read.csv("factory.csv", header = TRUE)
factory$process <- mapvalues(factory$공정, from = c(1,2),
to = c("기존공정","신공정"))
factory$rate <- mapvalues(factory$불량률, from = c(0,1),
to = c("정상","불량"))
table(factory$process) # 100 100
table(factory$rate)
table(factory$process, factory$rate)
prop.test(c(34,74), c(100, 100), alternative = "two.sided")
prop.test(c(34,74), c(100, 100), alternative = "less")


불량률이 정상일 때를 기준으로 prop.test 함수를 이용했다.
위 결과를 보면 p-value값이 0.05보다 작기 때문에 두 공정의 불량률의 차이가 나는 것을 볼 수 있다.
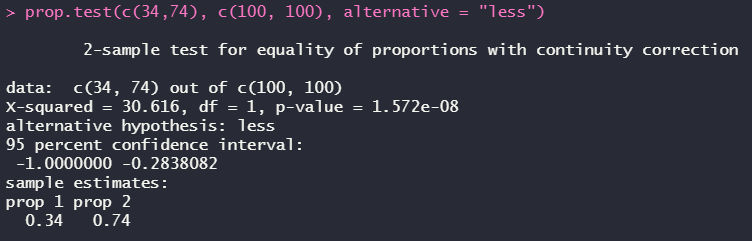
앞선 비율 검정을 통해 각 공정의 불량률이 다르다는 것을 알았다.
그렇다면 신공정이 더 불량률이 낮은 지를 확인하기 위해 prop.test 함수의 옵션 중 alternative="less"로 설정하여 비율 검정을 실시했다. 결과, p-value값이 0.05보다 작았다. 앞 값이(기존 공정)이 정상 비율이 더 작았다.
귀무가설을 기각하고 대립가설을 채택한다. 즉, 기존 공정에 비해 불량률이 변화하였다.(신공정이 불량률이 줄어들었다.)
문제2. 범주형 데이터와 연속형 데이터 처리하기

성별은 범주형 데이터이다. 학점은 연속형 데이터이다. 독립표본 t-test를 실시한다.
'성별에 따라 학점에 차이가 있을 것이다.'라는 가설을 세운다. 성별은 독립변수이고 학점은 종속변수다.
이상하게 정답이랑 답이 달랐다. 내 생각에는 데이터가 달라진 것 같다.
검정 결과가 달라진 이유가 mean값이 달라져서 그러는데 이건 나의 실수가 아니라고 생각한다.
소신껏 나의 답을 적겠다.
business = read.csv("business.csv", header = TRUE)
female <- subset(business, 성별 == 1)
male <- subset(business, 성별 == 2)
femaleCnt = length(female$성별)
femaleMean = round(mean(female$학점), 2)
maleCnt = length(male$성별)
maleMean = round(mean(male$학점), 2)
groupCnt <- c(femaleCnt, maleCnt) #288 212
groupMean <- c(femaleMean, maleMean) #3.59 3.55
groupTable = data.frame(Freq = groupCnt, Mean = groupMean)
var.test(female$학점, male$학점) # p-value = 0.06582
t.test(female$학점, male$학점, alther = "two.sided",
conf.int = TRUE, conf.level = 0.95) # p-value = 0.3849

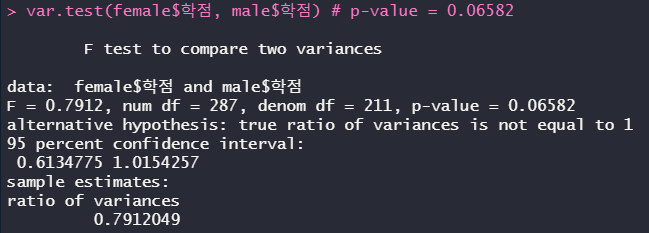
검정을 하기 전에 데이터가 정규분포를 이루는 지 확인해야 한다. var.test를 해줬다.
var.test를 다른 검정과 다르게 p-value가 0.05보다 커야지 모수 통계이다. 결과를 보면 모수통계이다.
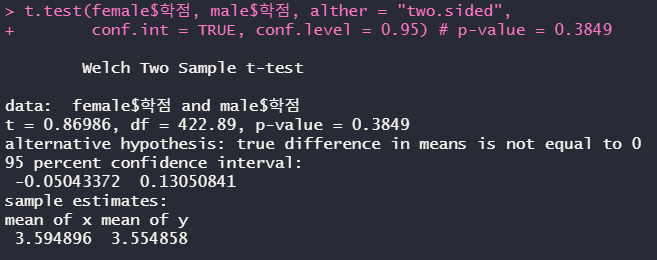
p-value값이 0.05보다 크므로 대립가설을 기각하고 귀무가설을 채택한다.
즉, 성별에 따라 학점의 차이가 없다.
문제3. 연속형 데이터 처리하기(변수 1개)

여기에서 필요한 변수는 학점이다. 성별은 필요가 없다. 변수가 1개이고 기준이 되는 수치(전국 평균 3.2점)가 있어서 one sample 이항 분포 검정을 이용한다. t-test를 사용한다.
'상경계열 학생들의 평균과 전국 평균이 차이가 있을 것이다.'라는 가설을 세운다.
business = read.csv("business.csv", header = TRUE)
mean(business$학점) #3.57792
range(business$학점) #1.3 4.5
length(business$학점) #500
shapiro.test(business$학점) #p-value = 1.54e-09 > 비모수 통계
t.test(business$학점, mu = 3.2) #p-value < 2.2e-16
t.test(business$학점, mu = 3.2, alter = "greater", conf.level = 0.95) #p-value < 2.2e-16
wilcox.test(business$학점, mu = 3.2, alter = "greater", conf.level = 0.95) #p-value < 2.2e-16
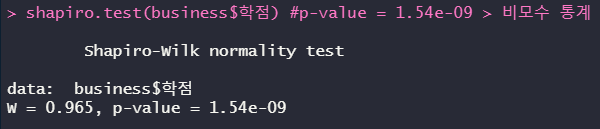
정규분포의 여부를 확인하기 위해 shapiro.test를 한다. 이것도 var.test와 같이 p-value값이 0.05보다 커야지 모수 통계를 할 수 있다. 결과를 보니 정규분포를 따르지 않는다. 비모수 통계를 해야 한다.
다만, 일반적으로 30명이 넘으면 암묵적으로 정규분포를 따른다고 가정하므로 t-test도 쓰고 wilcox.test도 썼다.
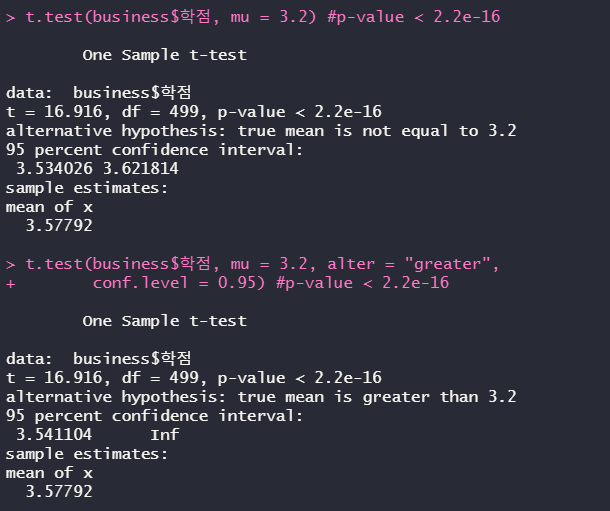
t-test를 했다. p-value값이 0.05보다 작기 때문에 두 값은 차이가 있다. t-test함수 중 옵션인 alternative = "greater"로 검정을 실시했다. 마찬가지로 p-value값이 0.05보다 작기 때문에 상경계 학생의 평균이 더 높은 걸 알 수 있다.

문제4. 범주형 데이터 처리하기(2)

가족의 수와 자동차의 크기는 범주형 데이터이다.
'가족구성원의 숫자에 따라서 차의 크기가 차이가 있을 것이다.' 가설을 설정한다.
가족의 수는 독립변수고 자동차의 크기는 종속변수다.
car = read.csv("carS.csv", header=TRUE)
chisq.test(car$family, car$carsize)
식은 간단하다.

p-value값이 0.05보다 작으므로 귀무가설을 기각하고 대립가설을 채택한다.
즉, 가족구성원 수에 따라 차 크기에 차이가 있다.
느낀점
과제를 제출하니 정답 풀이가 나왔다.
풀다보니 잘못 해석한 것이 있어서 고치는 시간을 가졌다.
확실히 과제를 푸니까 개념이해가 더 잘됐다. 나중에 블로그에 통계에 대해 다시 정리해야겠다.
마지막 모각코 끝!
'2020활동-1학년 > 2020 동계 모각코' 카테고리의 다른 글
| [모각코 후기] 동계모각코를 마치며 (0) | 2021.02.24 |
|---|---|
| [모각코 5회 회고록] 코드포스 대회/ 빅데이터 강의 듣기 (0) | 2021.01.27 |
| [모각코 4회 회고록] 코드포스 대회/ 빅데이터 강의 (0) | 2021.01.20 |
| [모각코 3회 회고록] 파이썬 빅데이터 교육듣기 (0) | 2021.01.13 |
| [모각코 2회 회고록] (0) | 2021.01.13 |



